Ohms lag för en komplett kedja och för en sektion av en kedja: alternativ för att skriva formel, beskrivning och förklaring

Det finns inget sätt för en professionell elektriker eller elektronikspecialist att kringgå Ohms lag i sin egen verksamhet och lösa eventuella problem relaterade till installation, justering och reparation av elektroniska och elektriska kretsar.

Egentligen måste alla förstå denna lag. För alla måste ta itu med el i vardagen.

Och även om den tyska fysikern Ohms lag föreskrivs i gymnasieskolans läroplan, studeras den i praktiken inte alltid i tid. Därför kommer vi i vårt material att överväga ett sådant relevant ämne för livet och förstå alternativen för att skriva formeln.

Ensektion och komplett elektrisk krets

Med tanke på en elektrisk krets ur synvinkeln att tillämpa Ohms lag på en krets, bör två möjliga beräkningsalternativ noteras: för en separat sektion och för en fullfjädrad krets.

Beräkning av strömmen i en elektrisk kretssektion

En del av en elektrisk krets anses som regel vara den del av kretsen som utesluter källan till EMF, eftersom den har ytterligare internt motstånd.

Därför ser beräkningsformeln, i det här fallet, enkel ut:

I = U/R,

Där respektive:

• jag – strömstyrka;
• U – pålagd spänning;
• R - motstånd.

Tolkningen av formeln är enkel - strömmen som flyter genom en viss del av kretsen är proportionell mot spänningen som appliceras på den, och motståndet är omvänt proportionellt.

Den så kallade grafiska "prästkragen", genom vilken hela uppsättningen av varianter av formuleringar baserade på Ohms lag presenteras. Bekvämt verktyg för fickförvaring: sektor "P" - effektformler; sektor "U" - spänningsformler; sektor "I" - nuvarande formler; sektor "R" - motståndsformler

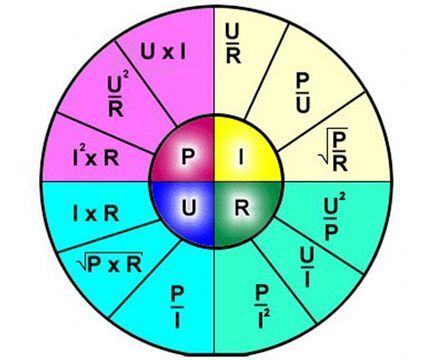
Således beskriver formeln tydligt beroendet av strömflödet genom en separat del av den elektriska kretsen i förhållande till vissa värden på spänning och motstånd.

Formeln är bekväm att använda, till exempel vid beräkning av parametrarna för motståndet som måste lödas in i kretsen om spänningen och strömmen är givna.

Ohms lag och två konsekvenser som varje professionell elektromekanisk ingenjör, elektroingenjör, elektronikingenjör och alla som är inblandade i driften av elektriska kretsar måste känna till. Från vänster till höger: 1 - aktuell bestämning; 2 - bestämning av motstånd; 3 - definition av spänning, där I - ström, U - spänning, R - motstånd

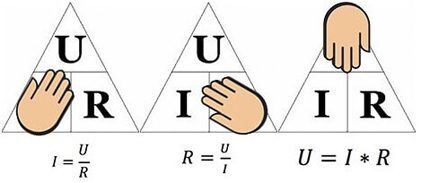
Ovanstående figur hjälper till att bestämma, till exempel, strömmen som flyter genom ett 10-ohm motstånd, till vilket en spänning på 12 volt appliceras. Genom att ersätta värdena finner vi – I = 12 / 10 = 1,2 ampere.

Problemen med att hitta resistans (när ström och spänning är kända) eller spänning (när spänningen och strömmen är kända) löses på liknande sätt.

Således kan du alltid välja önskad driftspänning, önskad strömstyrka och optimalt resistivt element.

Formeln som föreslås användas kräver inte att man tar hänsyn till spänningskällans parametrar.En krets som innehåller till exempel ett batteri kommer dock att beräknas med en annan formel. I diagrammet: A – slå på amperemetern; V – slå på voltmetern.

Förresten, anslutningstrådarna för alla kretsar är motstånd. Mängden belastning de måste bära bestäms av spänningen.

Följaktligen, återigen genom att använda Ohms lag, blir det möjligt att exakt välja det erforderliga ledartvärsnittet, beroende på kärnmaterialet.

Vi har detaljerade instruktioner på vår hemsida kabeltvärsnittsberäkning vad gäller kraft och ström.

Beräkningsmöjlighet för en komplett kedja

En komplett krets består av en sektion (sektioner), såväl som en källa för EMF. Det vill säga att den inre resistansen hos EMF-källan läggs till den existerande resistiva komponenten i kretssektionen.

Därför är det logiskt att ändra ovanstående formel något:

I = U / (R + r)

Naturligtvis kan värdet på den interna resistansen hos EMF i Ohms lag för en komplett elektrisk krets anses vara försumbar, även om detta resistansvärde till stor del beror på EMF-källans struktur.

Men vid beräkning av komplexa elektroniska kretsar, elektriska kretsar med många ledare, är närvaron av ytterligare motstånd en viktig faktor.

För beräkningar under förhållanden för en komplett elektrisk krets tas alltid hänsyn till EMF-källans resistiva värde. Detta värde summeras med den resistiva resistansen för själva den elektriska kretsen. I diagrammet: I - strömflöde; R—externt resistivt element; r är den resistiva faktorn för EMF (energikälla)

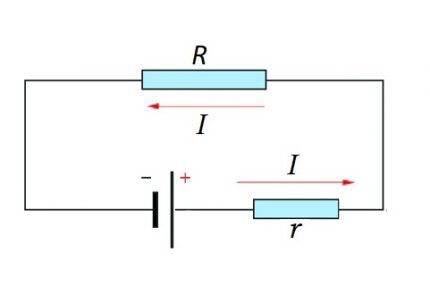
Både för en sektion av en krets och för en komplett krets bör det naturliga momentet beaktas - användningen av konstant eller variabel ström.

Om de ovan angivna punkterna, som är karakteristiska för Ohms lag, betraktades från synpunkten att använda likström, så ser allting med växelström något annorlunda ut.

Hänsyn till lagens inverkan på en rörlig storhet

Begreppet "motstånd" mot villkoren för att passera växelström bör betraktas mer som begreppet "impedans". Detta avser kombinationen av en resistiv belastning (Ra) och en reaktiv resistorbelastning (Rr).

Sådana fenomen orsakas av parametrarna för induktiva element och omkopplingslagarna i förhållande till ett variabelt spänningsvärde - ett sinusformat strömvärde.

Detta är den ekvivalenta kretsen för en elektrisk växelströmskrets för beräkning med hjälp av formuleringar baserade på principerna för Ohms lag: R - resistiv komponent; C är den kapacitiva komponenten; L—induktiv komponent; EMF är en energikälla; I - strömflöde

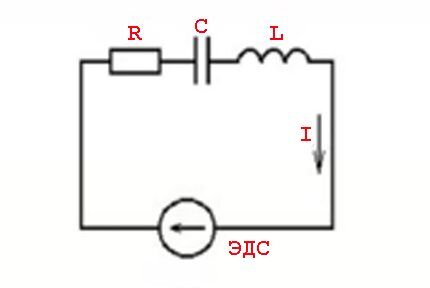
Med andra ord, det finns en effekt av strömvärden som leder (fördröjning) från spänningsvärden, vilket åtföljs av uppkomsten av aktiva (resistiva) och reaktiva (induktiva eller kapacitiva) krafter.

Sådana fenomen beräknas med formeln:

Z=U/I eller Z = R + J * (X_L -X_C)

Var: Z – impedans; R – aktiv belastning; X_L , X_C – induktiv och kapacitiv belastning; J - koefficient.

Seriell och parallell anslutning av element

För element i en elektrisk krets (sektion av en krets) är en karakteristisk punkt en seriell eller parallell anslutning.

Följaktligen åtföljs varje typ av anslutning av ett annat mönster av strömflöde och spänningsmatning.I detta avseende tillämpas också Ohms lag på olika sätt, beroende på möjligheten att inkludera element.

Krets av seriekopplade resistiva element

I förhållande till en seriekoppling (en sektion av en krets med två komponenter) används följande formulering:

• Jag = jag₁ = jag₂ ;
• U = U₁ +U₂ ;
• R = R₁ + R₂

Denna formulering visar tydligt att, oavsett antalet resistiva komponenter kopplade i serie, strömmen som flyter genom en sektion av kretsen inte ändras i värde.

Anslutning av resistiva element i en sektion av kretsen i serie med varandra. Detta alternativ har sin egen beräkningslag. I diagrammet: I, I1, I2 - strömflöde; R1, R2 - resistiva element; U, U1, U2 - pålagd spänning

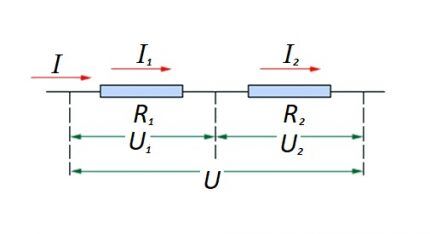
Storleken på spänningen som appliceras på de effektiva resistiva komponenterna i kretsen är summan och summerar värdet av emk-källan.

I detta fall är spänningen på varje enskild komponent lika med: Ux = I * Rx.

Det totala motståndet bör betraktas som summan av värdena för alla resistiva komponenter i kretsen.

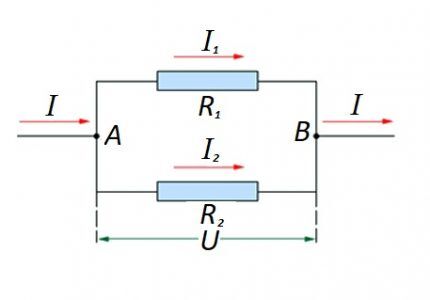
Krets av parallellkopplade resistiva element

I fallet när det finns en parallell koppling av resistiva komponenter, anses följande formulering vara rättvis i förhållande till den tyska fysikern Ohms lag:

• Jag = jag₁ +I₂ … ;
• U = U₁ = U₂ … ;
• 1/R = 1/R₁ + 1/R₂ + …

Alternativ för att skapa kretssektioner av "blandad" typ, när parallella och seriella anslutningar används, är inte uteslutna.

Anslutning av resistiva element på en sektion av en krets parallellt med varandra. För detta alternativ tillämpas en annan beräkningslag. I diagrammet: I, I1, I2 - strömflöde; R1, R2 - resistiva element; U är den tillförda spänningen; A, B - in-/utgångspunkter

För sådana alternativ utförs beräkningen vanligtvis genom att initialt beräkna parallellkopplingens resistiva betyg. Därefter läggs värdet på det seriekopplade motståndet till det erhållna resultatet.

Integrerade och differentiella former av lagen

Alla ovanstående punkter med beräkningar är tillämpliga på förhållanden när ledare av så att säga "homogen" struktur används i elektriska kretsar.

Samtidigt måste man i praktiken ofta ta itu med konstruktionen av scheman, där ledarnas struktur förändras i olika sektioner. Till exempel används ledningar med ett större tvärsnitt eller omvänt en mindre, gjorda av olika material.

För att ta hänsyn till sådana skillnader finns det en variation av den så kallade "differentialintegralen Ohms lag." För en infinitesimal ledare beräknas strömdensitetsnivån beroende på spännings- och konduktivitetsvärdet.

Följande formel används för differentialberäkning: J = ό * E

För integralberäkningen är formuleringen följaktligen: I * R = φ1 – φ2 + έ

Men dessa exempel ligger ganska närmare skolan för högre matematik och används faktiskt inte i den verkliga praktiken av en enkel elektriker.

Slutsatser och användbar video om ämnet

En detaljerad analys av Ohms lag i videon nedan kommer att hjälpa till att äntligen konsolidera kunskap i denna riktning.

En unik videolektion förstärker kvalitativt den teoretiska skriftliga presentationen:

En elektrikers arbete eller en elektronikingenjörs verksamhet är integrerat kopplat till ögonblick då man faktiskt måste följa Georg Ohms lag i handling. Det här är någon sorts truismer som alla professionella borde känna till.

Omfattande kunskap om denna fråga krävs inte - det räcker att lära sig de tre huvudvarianterna av formuleringen för att framgångsrikt tillämpa den i praktiken.

Vill du komplettera ovanstående material med värdefulla kommentarer eller uttrycka din åsikt? Skriv gärna kommentarer i blocket under artikeln. Om du har några frågor, tveka inte att fråga våra experter.